L'oeil et la vision |
|
Nous pourrions penser que notre oeil est le meilleur photoscope qu'il soit
et qu'il surpasse en tous points ceux des meilleurs grands fabriquants. En fait
il n'en est rien et un simple jetable est beaucoup plus performant.
La distance focale de notre oeil est d'environ 16mm avec une ouverture variant
de f/2 à f/11 selon les conditions lumineuses. Il est constitué de trois lentilles
en un groupe: la cornée, l'humeur aqueuse et le cristallin. Oui, je dis bien que la cornée
et l'humeur aqueuse sont des lentilles et vous comprendrez pourquoi lors de la definition
de ce qu'est une lentille. En revanche, je ne considère pas l'humeur vitreuse comme telle
car elle est en contact direct avec la rétine ; quoi que...
La cornée est donc une lentille avec un indice de réfraction de 1.376 et l'humeur aqueuse avec un indice de 1.336. L'humeur vitreuse a un indice de 1.337 mais comporte beaucoup de particules opaques. Ces indices de réfraction sont très proche; la réfraction est donc très légère, mais elle existe. La réfraction à l'interface air-cornée est en revanche forte. Réflechissez sur la question suivante: pourquoi ne voyont nous pas sous l'eau dont l'indice est de 1.333 ? L'indice de réfraction du cristallin n'est pas homogène et varie de 1.386 à 1.406 de la périphérie au centre. Je disais que l'oeil était un mauvais photoscope mais il faut admettre qu'il possède une formidable lentille. L'industriel réussissant à couler un verre comme le cristallin aura vraiment gagné le gros lot. La rétine constitue le 'film' de notre photoscope naturel. Elle comporte environ 125 millions de récepteurs, les bâtonnets, incapable d'analyser les couleurs mais très sensibles à la lumière; et environ 6 millions de récepteurs couleurs, les cônes, de faible sensibilité. Le domaine des longueurs d'onde visibles par ces cellules est ce que nous appellons la lumière et s'étant de 390nm à 780nm. L'arrivée du nerf optique forme le point noir où il n'existe aucun récepteur. Nous sommes donc aveugles au beau milieu de la rétine juste en dessous de l'axe optique. L'axe visuel, juste au dessus de l'axe optique, ne comporte que des cônes dont la forte densité permet d'avoir une très bonne définition dans cette petite région de 0.3mm de diamètre. Pour finir, toute la connectique n'est pas sous le plancher de la rétine mais directement au dessus des récepteurs en contact avec l'humeur vitreuse. Dame Nature, quelle drôle d'idée ! Alors pourquoi voyons-nous si bien ? Tout simplement parce que c'est ce que nous croyons faute d'un autre système de vision à notre disposition pour comparaison et parce que notre cerveau effectue un formidable traitement de l'information. |
Optique & Géométrie |
Un objet peut être source de lumière (par exemple un fil métallique incandescent) et nous
parlons de source primaire ; ou bien peut simplement réflechir la lumière et nous parlons alors
de source secondaire. Dans les deux cas, le résultat visuel est le même; chaque point, chaque atome
de l'objet émet dans tout l'espace des ondes lumineuses. Nous voyons un objet parce que nous
voyons chaques points qui le construisent. Comment ?
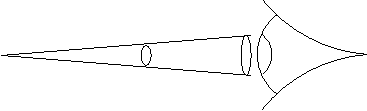 Fig.I Fig.I
De chacun des points qui compose la surface d'un objet (en supposant que ce dernier est opaque), nous recevons un cône d'ondes lumineuses dont la base est définie par le diamètre de la pupille. Ces ondes lumineuses, traversant la pupille, convergent alors vers un seul point de la rétine. Notre oeil a ainsi transformé un point objet en un point image ; un objet en une image que les récepteurs de la rétines transforment en signaux électriques. Il est très important de comprendre ce que je viens de décrire pour comprendre la suite. Résumons : de chaque point d'un objet divergent une infinité d'ondes lumineuses traversant l'espace en ligne droite et ceci dans tout l'espace. Une partie de ces ondes traverse alors notre oeil. Ce système optique les fait converger vers un seul point de notre rétine. Toujours pour mieux comprendre, supposons un oeil sans lentilles, formé simplement par une rétine.  Fig.II Fig.II
Chaque capteur (cône ou bâtonnet) de la rétine reçoit d'un point objet un cône d'ondes lumineuses dont la base correspond au diamètre du capteur. Jusque-là tout va bien. Le problème est que ce même capteur reçoit aussi un cône d'ondes de tous les points objets et ceci pour tous les objets se trouvant dans la demi-sphère visible par la rétine. Bref la rétine voit, mais ne voit qu'une lumière uniforme à l'instar d'un capteur hémisphérique de flashmètre! A partir d'ici, si vous n'êtes pas familier avec les bases de l'optique, je vous conseille la lecture d'un ouvrage traitant du sujet. Un livre de second cycle est largement suffisant. Il faut simplement connaître la géométrie de la formation d'une image. Savoir par exemple que tout rayon passant par le centre optique de la lentille n'est pas dévié. |
Regardons tout d'abord le dessin ci-dessous. Il résume toute cette géométrie pour une lentille convergente.
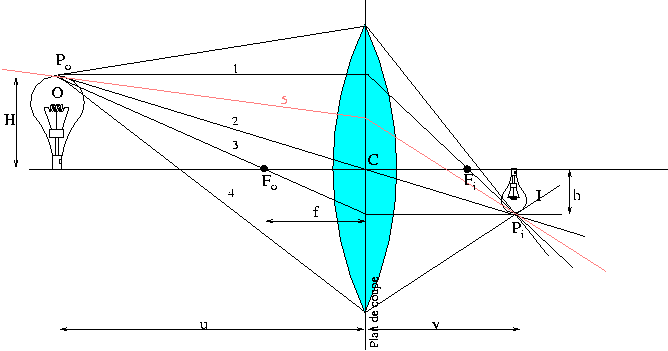 Fig.III Fig.III
O est un objet, ici une ampoule et I est son image construite par une simple lentille convergente. Nous avons vu que chaque entité (atome ou molécule) de l'ampoule émet dans tout l'espace un rayonmment électromagnétique. Supposons que Po est l'une de ces entités. Ce point objet émet donc dans tous l'espace; mais une partie du rayonnement atteint la surface de la lentille. Cette partie de rayonnement est délimité par un angle solide (un cône) donc la base est la lentille. De tout ce flux photonique, le dessin nous montre trois propriétés de la lentille. Ces trois trajectoires particulières passent toutes par un seul point, le point image Pi. Je postule alors que tout rayon (4) partant de, ou passant par Po et traversant la lentille est dévié pour passer par Pi. Deux choses importante ici. Je parle de rayon passant par Po. C'est très important de comprendre que pour la lentille, Po n'a rien d'un point matériel. Elle ne différencie pas un photon émanant de Po d'un photon passant par Po. De même Pi n'est pas une sorte de piège où tous les photons s'agglutinent. C'est simplement un point de l'espace où passe des photons. Voir le rayon (5) sur le dessin. Ainsi si l'on place une deuxième lentille après l'image de l'ampoule, Pi devient pour cette lentille un nouveau Po. Je dois aussi rajouter qu'il faut avoir une représentation en 3D de ce dessin. Po peut alors être un point à l'extérieur de l'écran (le plan de coupe du dessin). Le rayon (3), par exemple, traverse alors l'écran en Fo et atteint ensuite la lentille sur une partie située derrière le plan de coupe. La suite, vous la connaissez... Maintenant regardons ce qui ce passe si nous bougeons l'objet O.  Fig.IV Fig.IV
Plus O est éloigné de la lentille, plus I est petit et proche de Fi. Si O est à l'infinie, on peut considérer que tous les photons atteignent la lentille perpendiculairement au plan de coupe. I est alors infiniment petit et se confond avec Fi. Mais attention, une photo de paysage à l'infinie ne se réduit pas à un seul point image car le paysage est formé d'une infinité de points dont les rayons ne sont pas nécessairement perpendiculaires au plan de coupe. Il en resulte la formation d'une image sur un plan passant par Fi que l'on nomme le plan focale image. C'est un plan limite et aucune image nette ne peut exister entre la lentille et ce plan. 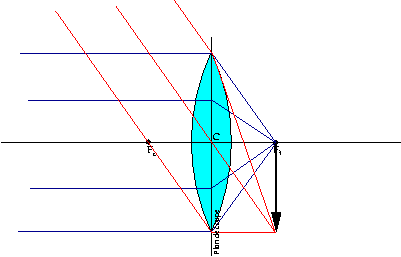 Fig.V Fig.V
En inversant ce dernier dessin, nous voyons que l'image d'un objet (plat) placé sur le plan focale objet est à l'infinie et il n'existe aucune image d'objet placé entre Fo et la lentille. Maintenant, à partir de ce que nous savons, expliquons pourquoi une lentille convergente grossie la taille des objets. Mais a-t'elle vraiment un pouvoir grossissant ? La figure IV semble nous dire qu'il en est pas toujours ainsi. En effet en fonction de la position de l'objet, son image peut être plus grande ou plus petite que celui-ci. Donc une lentille convergente n'est pas nécessairement grossissante. Nous pouvons en apporter très simplement la preuve avec de simple calcul de trigonométrie. Je vous donne ci-dessous les formules en posant m=v/u=h/H où m est le rapport de reproduction. u = f(1 + 1/m) v = f(1 + m) L'image a donc la même taille (m=1) losrque l'objet se trouve à deux fois la distance focale du centre optique. Si l'objet est plus proche, son image est plus grande et si l'objet est plus loin, son image est plus petite. Pourtant ma loupe de bureau qui est une simple lentille convergente grossie bien les objets. Alors quel est le phénomène mis en jeu ? N'y-a-t'il pas une grande différence entre la figure III et ce que nous voyons avec une loupe de bureau ? En fait avec ma loupe de bureau, les objets sont agrandis mais pas inversés. Ce n'est donc pas l'image formée par la loupe que nous voyons mais bien l'objet lui-même. Donc, dans cette façon d'utiliser une loupe, l'oeil n'est pas un simple instrument de mise en évidence des phénomènes optiques. Il fait partie intégrante du système optique. Loupe et oeil forment un nouvel objectif beaucoup plus puissant que l'oeil seul. La figure ci-dessous montre deux configurations représentant approximativement un tel système.  Fig.VI
P, qui est simplement l'inverse de la focale, est la puissance exprimée en dioptrie. Dans le cas simple de deux lentilles en contact, nous
voyons que la puissance sera toujours supérieure à la puissance de l'oeil seul (B). Fig.VI
P, qui est simplement l'inverse de la focale, est la puissance exprimée en dioptrie. Dans le cas simple de deux lentilles en contact, nous
voyons que la puissance sera toujours supérieure à la puissance de l'oeil seul (B).
Nous pouvons facilement dessiner le trajet des rayons lumineux dans un cas particulier où le point focale objet de B coïncide avec le centre optique de A. 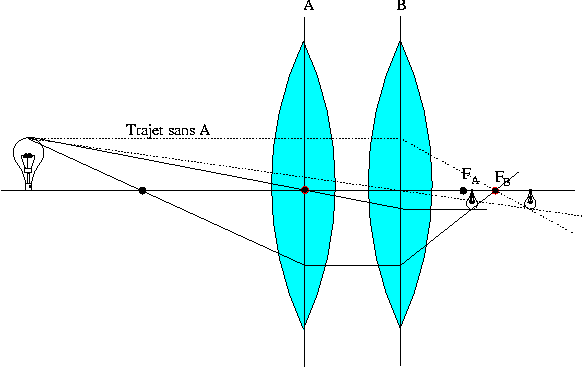 Fig.VII Fig.VII
Comme d = Fb; P = Pa. Le dessin le prouve avec deux images de taille identique. Vous allez me dire que l'image est à l'envers. Oui, mais c'est l'image formée sur la rétine qui dans tous les cas sera toujours inversée. C'est notre cerveau qui rétablie tout! |
Maintenant à moi de vous prouver que tous les phénomènes optiques mis en jeu dans un objectif ne sont que le résultat de la réfraction.
Nous avons déja vu dans "La Lumière" ce qu'est la réfraction. A chaque interface entre deux mileux dont les indices de réfraction
sont différents, les photons sont déviés. Cette réfraction (déviation)
des rayons lumineux suit la loi de Snell :

Supposons une lentille convergente élémentaire composée d'une seule surface sphérique de réfraction. Ce type de lentille existe! Un poisson rouge, gagné à la foire, regarde toujours la chambre de son nouveau propriétaire à travers ce type de lentille qu'est son bocal. Prouvons géométriquement et en suivant la loi de Snell que tous rayons parallèles à l'axe SCI converge vers un point fixe I. Le dessin ci-dessous illustre un tel parcours lumineux. 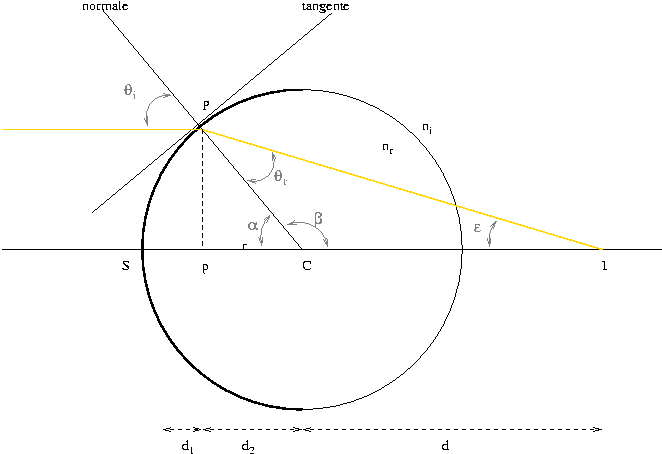
Un rayon incident (en jaune), parallèle à SCI, atteint le point P de la surface sphérique. Pour le photon, infiniment petit, le rayon de courbure de la surface est infiniment grand et la surface peut être considerée comme plane. La loi de Snell est donc directement applicable. Soit |SC| le rayon de courbure r de la surface et |CI| la distance notée d, admettons que la distance focale f est la somme de r et d. La géométrie euclidienne postule que la somme des angles d'un triangle est toujours égale à 180°. Soit, 


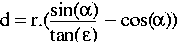

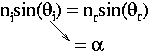
Pour simplifier les calculs, suppossons que les angles sont petits. Nous pouvons alors écrire : 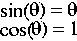
(Mais rien ne vous empêche d'être rigoureux et de poursuivre le calcul avec sin() et cos()). La relation de Snell est alors beaucoup plus simple à écrire : 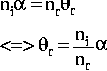

Les calculs ci-dessus n'ont fait appel qu'à la relation de Snell et à la trigonométrie. Nous en déduisons finalement la distance focale : 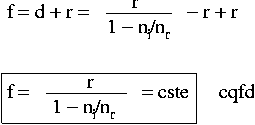
L'expression de la distance focale ne comporte que des constantes. f est donc constante quelque soit la position de P sur la surface. Nous avons démontré l'une des propriétés optiques des lentilles; à savoir que tout rayon lumineux parallèle à l'axe optique converge vers un seul point nomé point focale image. Vous pouvez maintenant faire les calculs pour un rayon lumineux non parallèle à SCI et trouver le même résultat. Mais une lentille, c'est bien plus qu'une simple surface sphérique ? Oui en effet, c'est en fait deux surfaces sphériques et la calcul est presque pas plus compliqué ! 
A vous de trouver la formule générale des constructeurs de lentilles. |